Kaggle Competition: Digit recognition on MNIST data

7/7/2017 Wei-Ying Wang

This is my tutorial about how to use Keras to construct a CNN model for digit recognition. The tutorial tried to be comprehensive about building CNN with Keras. Keras is designed to be easy to use and manipulate, however I found difficult to understand the structure I built when I first used it. I hope this tutorial can help smooth the learning curve of using Keras.

Most of the information is on chapter 2 and 3. I will emphasize a lot on knowing the number of parameters, inputs, and outputs.

To use this Ipython notebook, please download the data train.csv and test.csv from Kaggle Digit Recognizer webpage, and put it into the right directory.

I eventually got 99.21% correction rate. Note that MNIST dataset is famous online, and it is not surprising that one can get 100% on the test set provided by Kaggle, since it is not difficult to find all the MNIST data somewhere else. The real winner (correct me if I am wrong) so far is from Dan Cireşan et. al. 2012, who got 99.77% correction rate, which achieved near human performance. He used CNN, too.

Table of content

1. Import modules and preprocessing the data

2. A Typical CNN structure: one CNN layer

3. Stack more CNN layers

4. Using the learned trained model to predict the test set

You can download this Ipython notebook at My Github Website.

1. Import modules and preprocessing the data

from importlib import reload

from __future__ import print_function
import keras
import numpy as np
import matplotlib.pyplot as plt
from keras.models import Sequential
from keras.layers import Dense, Dropout,Flatten,Conv2D, MaxPooling2D
from keras.optimizers import RMSprop
from keras.utils.np_utils import to_categorical
#from keras.preprocessing.image import ImageDataGenerator
import pandas as pd
from sklearn.model_selection import train_test_split
import Aux_fcn
reload(Aux_fcn)

Using TensorFlow backend.





<module 'Aux_fcn' from 'D:\\Dropbox\\Job finding\\Some machine learning topic\\code\\MNIST_Kaggle\\github\\Aux_fcn.py'>

Import the data ( Download at https://www.kaggle.com/c/digit-recognizer/data), and be sure to put it into the right place.

train = pd.read_csv('../data/train.csv')
test  = pd.read_csv('../data/test.csv')

train.head()
label pixel0 pixel1 pixel2 pixel3 pixel4 pixel5 pixel6 pixel7 pixel8 ... pixel774 pixel775 pixel776 pixel777 pixel778 pixel779 pixel780 pixel781 pixel782 pixel783
0 1 0 0 0 0 0 0 0 0 0 ... 0 0 0 0 0 0 0 0 0 0
1 0 0 0 0 0 0 0 0 0 0 ... 0 0 0 0 0 0 0 0 0 0
2 1 0 0 0 0 0 0 0 0 0 ... 0 0 0 0 0 0 0 0 0 0
3 4 0 0 0 0 0 0 0 0 0 ... 0 0 0 0 0 0 0 0 0 0
4 0 0 0 0 0 0 0 0 0 0 ... 0 0 0 0 0 0 0 0 0 0

5 rows × 785 columns

test.head()
pixel0 pixel1 pixel2 pixel3 pixel4 pixel5 pixel6 pixel7 pixel8 pixel9 ... pixel774 pixel775 pixel776 pixel777 pixel778 pixel779 pixel780 pixel781 pixel782 pixel783
0 0 0 0 0 0 0 0 0 0 0 ... 0 0 0 0 0 0 0 0 0 0
1 0 0 0 0 0 0 0 0 0 0 ... 0 0 0 0 0 0 0 0 0 0
2 0 0 0 0 0 0 0 0 0 0 ... 0 0 0 0 0 0 0 0 0 0
3 0 0 0 0 0 0 0 0 0 0 ... 0 0 0 0 0 0 0 0 0 0
4 0 0 0 0 0 0 0 0 0 0 ... 0 0 0 0 0 0 0 0 0 0

5 rows × 784 columns

print('training data is (%d, %d) and test data is (%d, %d).'% (train.shape+test.shape))

training data is (42000, 785) and test data is (28000, 784)

#%%
X_train_all = (train.ix[:,1:].values).astype('float32')/255 # all pixel values, convert to value in [0,1]
y_train_all = train.ix[:,0].values.astype('int32') # only labels i.e targets digits
y_train_all= to_categorical(y_train_all) # This convert y into onehot representation
X_test = (test.values).astype('float32')/255 # all pixel values
X_train, X_val, y_train, y_val = train_test_split(X_train_all, y_train_all, test_size=0.10, random_state=42)

We have to map the image vectors (size 784) back to image. Specially, we have to convert to (28,28,1), since the convolution layer of Kares only accept image of dimension 3 (the last dim is the color channel).

X_train_img=np.reshape(X_train,(X_train.shape[0],28,28,1))
X_test_img = np.reshape(X_test,(X_test.shape[0],28,28,1))
X_val_img = np.reshape(X_val,(X_val.shape[0],28,28,1))

plt.imshow(X_train_img[0,:,:,0],cmap = 'gray')
plt.show()

png

---------------------------------------------------------------------------

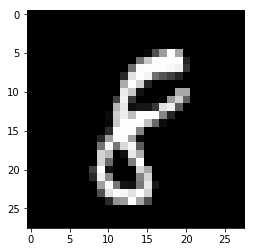
TypeError                                 Traceback (most recent call last)

<ipython-input-5-9ad6acbe2367> in <module>()
      1 plt.imshow(X_train_img[0,:,:,0],cmap = 'gray')
      2 plt.show()
----> 3 plt.imsave('one_training_sample.png')


C:\WinPython-64bit-3.6.0.1Qt5\python-3.6.0.amd64\lib\site-packages\matplotlib\pyplot.py in imsave(*args, **kwargs)
   2318 @docstring.copy_dedent(_imsave)
   2319 def imsave(*args, **kwargs):
-> 2320     return _imsave(*args, **kwargs)
   2321 
   2322 


TypeError: imsave() missing 1 required positional argument: 'arr'

2. A Typical CNN structure: one CNN layer.

  1. The original input image is $28\times28$, so the input_shape=(28,28,1), where 1 indicates that number of color channels is 1.

  2. In the following convolution layer, there are 32 filters, and each filters is $3\times3$.

    • You can set border differently by: 
         border_mode='same', 'fall', or 'valid' (default)
    • With valid border, after convolution (with stride=0), the filted image size is (28-2)x(28-2) = 26x26
  1. There are $32\cdot3\cdot3+32 =320$ parameters.
    • Each “pixel” of the filted (and subsampled) image is obatained by $\sum_{i=1}^9 w_i x_i +b$, where $w_1,…,w_9,b\in \mathbb{R}^{10}$ are parameters and $(x_1,…,x_9)$ is a $3\times3$ image patches in the original input image.

  2. Using relu units by activation='relu', then max Pooling by 2. So the output of this CNN layer will be $32$ of $6\times 6$ “images”.

  3. If the next layer is ‘softmax’, one has to ‘flatten’ the output of the CNN layer. After flatten, the input of the next layer is of $6\cdot 6\cdot 32=1152$ values.

  4. So the last layer (‘softmax’) would require $1152\cdot 10+10$ parameters.
model = Sequential()
model.add(Conv2D(32, 3, 3,
                 activation='relu',subsample=(2,2),
                 input_shape=(28,28,1)))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Flatten(name='flatten'))
model.add(Dense(10, activation='softmax'))
model.summary()

____________________________________________________________________________________________________
Layer (type)                     Output Shape          Param #     Connected to                     
====================================================================================================
convolution2d_1 (Convolution2D)  (None, 13, 13, 32)    320         convolution2d_input_1[0][0]      
____________________________________________________________________________________________________
maxpooling2d_1 (MaxPooling2D)    (None, 6, 6, 32)      0           convolution2d_1[0][0]            
____________________________________________________________________________________________________
flatten (Flatten)                (None, 1152)          0           maxpooling2d_1[0][0]             
____________________________________________________________________________________________________
dense_1 (Dense)                  (None, 10)            11530       flatten[0][0]                    
====================================================================================================
Total params: 11,850
Trainable params: 11,850
Non-trainable params: 0
____________________________________________________________________________________________________

Before fitting the parameters, we need to compile the model first.

model.compile(loss='categorical_crossentropy',
              optimizer='RMSprop',
              metrics=['accuracy'])

We can now fit the parameters. Note that:

batch_size = 64 
epochs = 20 
history = model.fit(X_train_img, y_train,
                    batch_size=batch_size,
                    nb_epoch=epochs,
                    verbose=2, 
                    validation_data=(X_val_img, y_val),
                    initial_epoch=10)

Train on 37800 samples, validate on 4200 samples
Epoch 11/20
3s - loss: 0.0478 - acc: 0.9864 - val_loss: 0.0749 - val_acc: 0.9764
Epoch 12/20
3s - loss: 0.0464 - acc: 0.9865 - val_loss: 0.0753 - val_acc: 0.9764
Epoch 13/20
3s - loss: 0.0453 - acc: 0.9872 - val_loss: 0.0741 - val_acc: 0.9769
Epoch 14/20
3s - loss: 0.0440 - acc: 0.9876 - val_loss: 0.0754 - val_acc: 0.9762
Epoch 15/20
3s - loss: 0.0431 - acc: 0.9880 - val_loss: 0.0731 - val_acc: 0.9769
Epoch 16/20
3s - loss: 0.0418 - acc: 0.9880 - val_loss: 0.0730 - val_acc: 0.9748
Epoch 17/20
3s - loss: 0.0413 - acc: 0.9888 - val_loss: 0.0766 - val_acc: 0.9755
Epoch 18/20
3s - loss: 0.0398 - acc: 0.9888 - val_loss: 0.0767 - val_acc: 0.9769
Epoch 19/20
3s - loss: 0.0394 - acc: 0.9891 - val_loss: 0.0763 - val_acc: 0.9779
Epoch 20/20
3s - loss: 0.0384 - acc: 0.9892 - val_loss: 0.0759 - val_acc: 0.9764

We can see that after 20 epoch, the validation accuracy is not improved (around 97.6%). The training set accuracy is about 98.8%. We should first try more complicated model to see if the training set accuracy get higher.

3. Stack more CNN layers

In the following model, we have:

1. First CNN layer:

2. Second CNN layer:

3. Third: MaxPool layer:

4. Forth: A normal nural network layer with 128 nodes

5. Fifth: Flatten the output of the previous layer:

6. Final: 10 softmax units.

model = Sequential()
model.add(Conv2D(64, 5, 5,
                 activation='relu',
                 input_shape=(28,28,1)))
model.add(Conv2D(32, 3, 3, activation='relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Dense(128, activation='relu'))
model.add(Dropout(0.2))   
model.add(Flatten(name='flatten'))
model.add(Dense(10, activation='softmax'))
model.summary()
model.compile(loss='categorical_crossentropy',
              optimizer='RMSprop',
              metrics=['accuracy'])

____________________________________________________________________________________________________
Layer (type)                     Output Shape          Param #     Connected to                     
====================================================================================================
convolution2d_12 (Convolution2D) (None, 24, 24, 64)    1664        convolution2d_input_7[0][0]      
____________________________________________________________________________________________________
convolution2d_13 (Convolution2D) (None, 22, 22, 32)    18464       convolution2d_12[0][0]           
____________________________________________________________________________________________________
maxpooling2d_7 (MaxPooling2D)    (None, 11, 11, 32)    0           convolution2d_13[0][0]           
____________________________________________________________________________________________________
dense_12 (Dense)                 (None, 11, 11, 128)   4224        maxpooling2d_7[0][0]             
____________________________________________________________________________________________________
dropout_6 (Dropout)              (None, 11, 11, 128)   0           dense_12[0][0]                   
____________________________________________________________________________________________________
flatten (Flatten)                (None, 15488)         0           dropout_6[0][0]                  
____________________________________________________________________________________________________
dense_13 (Dense)                 (None, 10)            154890      flatten[0][0]                    
====================================================================================================
Total params: 179,242
Trainable params: 179,242
Non-trainable params: 0
____________________________________________________________________________________________________

batch_size = 64
epochs = 5
history = model.fit(X_train_img, y_train,
                    batch_size=batch_size,
                    nb_epoch=epochs,
                    verbose=2, # verbose controls the infromation to be displayed. 0: no information displayed
                    validation_data=(X_val_img, y_val),
                    initial_epoch=0)


Train on 37800 samples, validate on 4200 samples
Epoch 1/5
104s - loss: 0.1609 - acc: 0.9504 - val_loss: 0.0661 - val_acc: 0.9793
Epoch 2/5
104s - loss: 0.0577 - acc: 0.9828 - val_loss: 0.0519 - val_acc: 0.9848
Epoch 3/5
104s - loss: 0.0435 - acc: 0.9867 - val_loss: 0.0411 - val_acc: 0.9883
Epoch 4/5
104s - loss: 0.0370 - acc: 0.9884 - val_loss: 0.0497 - val_acc: 0.9848
Epoch 5/5
105s - loss: 0.0317 - acc: 0.9902 - val_loss: 0.0411 - val_acc: 0.9867

The following function shows the wrongly predicted images. Many of them I can’t even tell what it is…

Aux_fcn.plot_difficult_samples(model,X_val_img,y_val,verbose=False)
plt.show()

4200/4200 [==============================] - 4s     
There are 56 wrongly predicted images out of 4200 validation samples

png

4. Using the learned trained model to predict the test set.

pred_classes = model.predict_classes(X_test_img)

28000/28000 [==============================] - 30s      - ETA: 20s - ETA: 2s

i=10
plt.imshow(X_test_img[i,:,:,0],cmap='gray')
plt.title('prediction:%d'%pred_classes[i])
plt.show()

png

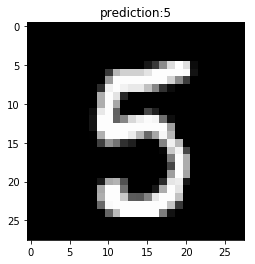
Appendix:

The function Aux_fcn.plot_difficult_samples is the following:

def plot_difficult_samples(model,x,y, verbose=True):
    """
    x: size(n,h,w,c)
    y: is categorical, i.e. onehot, size(n,p)
    """ 
    #%%
    
    pred_classes = model.predict_classes(x)
    y_val_classes = np.argmax(y, axis=1)
    er_id = np.nonzero(pred_classes!=y_val_classes)[0]
    #%%
    K = np.ceil(np.sqrt(len(er_id)))
    fig = plt.figure()
    print('There are %d wrongly predicted images out of %d validation samples'%(len(er_id),x.shape[0]))
    for i in range(len(er_id)):
        ax = fig.add_subplot(K,K,i+1)
        k = er_id[i]
        ax.imshow(x[er_id[i],:,:,0])
        ax.axis('off')
        if verbose:
            ax.set_title('%d as %d'%(y_val_classes[k],pred_classes[k]))