Prototype Learning: Generalized K-means
Wei-Ying Wang and Stuart Geman, 2017
How to learn the inherent structures of data (unsupervisedly)? Our algorithm can do it pretty well! In the right plot, after we found 3 structures (AKA prototypes) we summarized the data point according to its nearest structure, and group them by different colors.
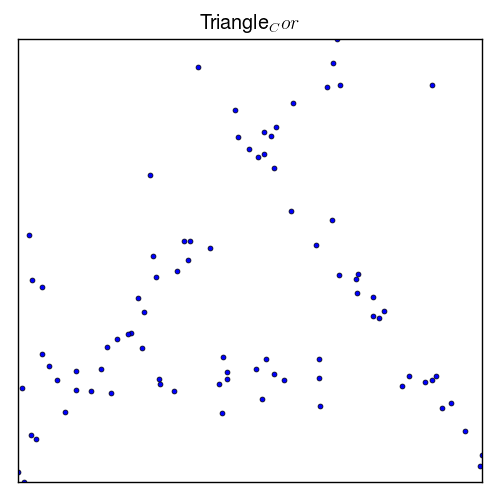 |
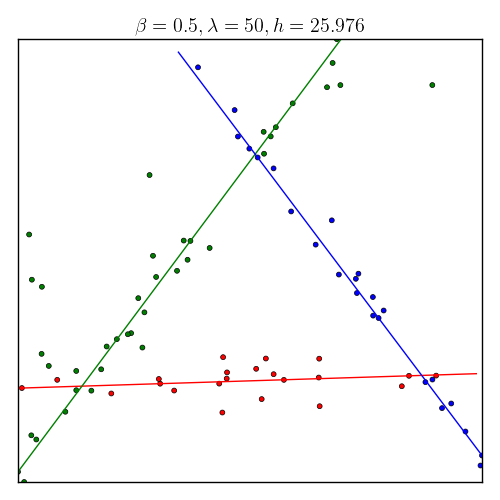 |
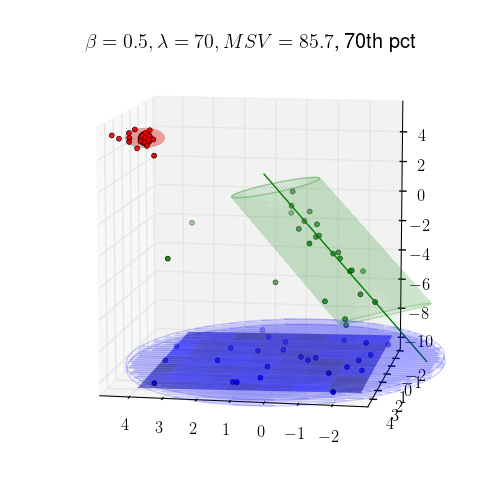
Another example in 3D:
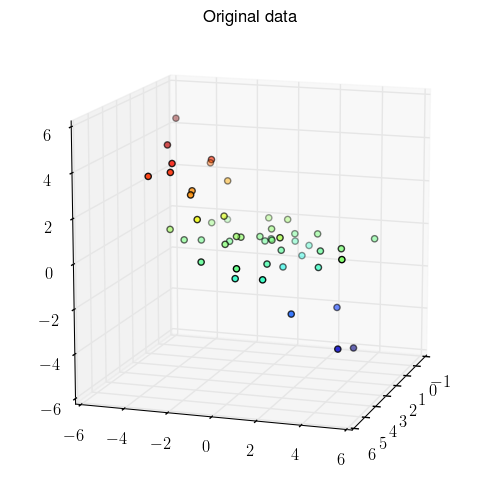 |
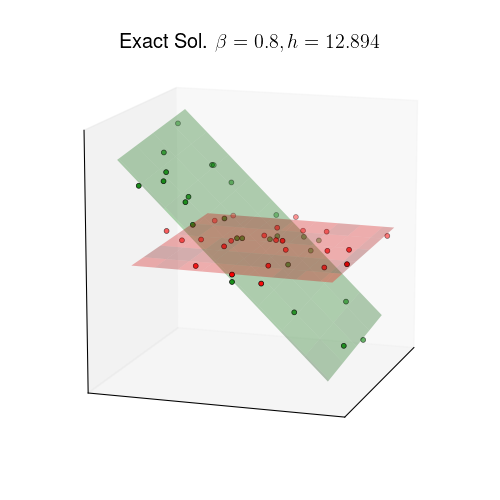 |
Our idea is to generalize the loss function of K-means (minimizing it is an NP-hard problem!) and minimize it. However, direct generalizing the idea of K-means algorithm is NOT working. Instead, we characterize a property of the minimizer and built an algorithm that approximate it. In nearly all our experiments, the algorithm work found the exact minimizer of our loss function wonderfully.
The traditional way of finding these structures is using EM algorithm with Gaussian model, which is very similar to that of K-means, however, it fails horribly once we add some outliers to the data.
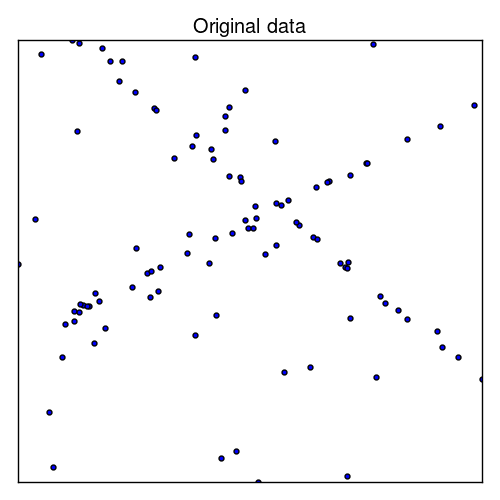 |
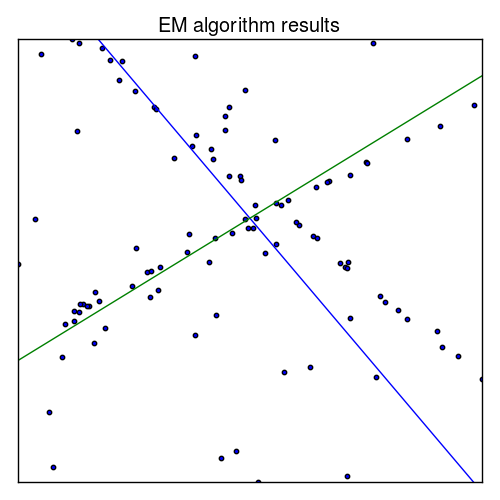 |
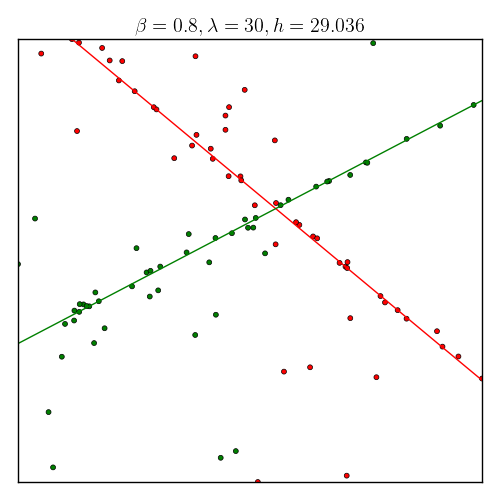 |
Let’s look another example, which has more outliers, to demonstrate the robust nature of our method.
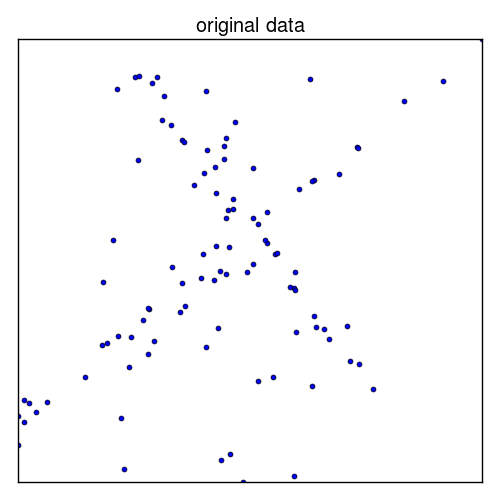 |
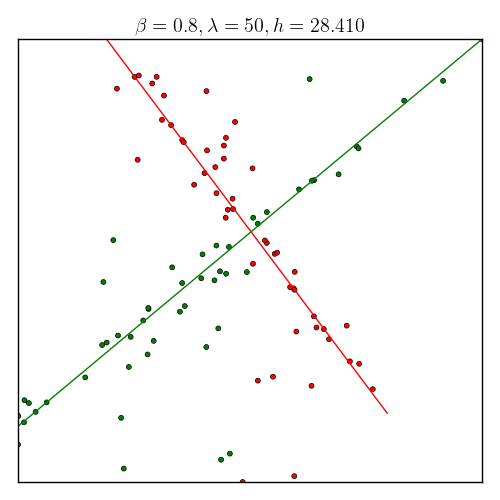 |
How about finding multiple different structures? Our algotihm can do it with some little “twist.” The “twist” is to use an idea of minimal volume of a cluster. In the following plots, the right one shows the structures our algorithm found, we put two circle and a rectangle to give reader the idea of minimum volumes. For example: the volume of a point cluster (cluster that closes to a point structure) is defined as the area of a circle.
 |
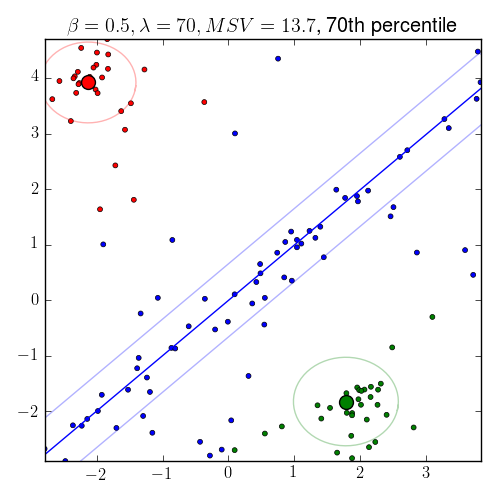 |
An example in 3D:
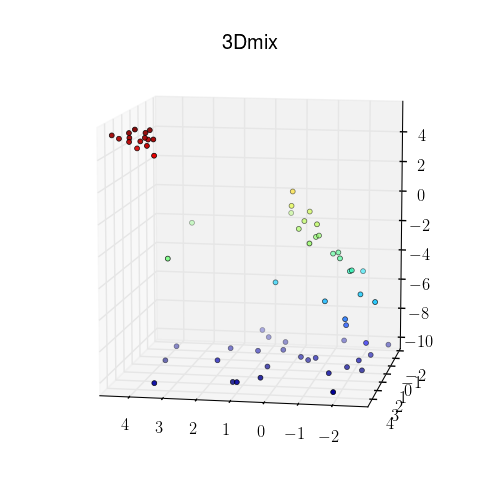 |
 |
By the way, we have a rule of thumb to determine the number of structures.